Answer:
x = 68
Step-by-step explanation:
Given equation:
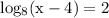
To Find:
Value of x
Solution:
Rewrite the equation in exponential form which is equivalent to b^y = x.
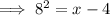
Now find the value of x.
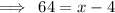
Transpose 4 from RHS to LHS, make sure to change its sign from (-) to (+) .
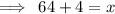
Overturn the equation
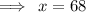
Thus, value of x is 68.