Answer:
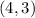 and
and
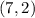 do not lie on the line
do not lie on the line
Explanation:
Given
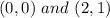
Required
Determine which points that are not on the line
First, we need to determine the slope (m) of the line:
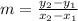
Where
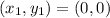
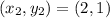
So;
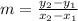

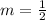
Next, we determine the line equation using:

Where
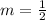
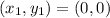
 becomes
becomes
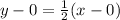

To determine which point is on the line, we simply plug in the values of x to in the equation check.
For
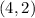
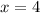 and
and
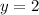
Substitute 4 for x and 2 for y in

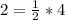
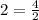

This point is on the graph
For
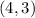
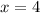 and
and
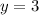
Substitute 4 for x and 3 for y in


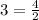
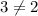
This point is not on the graph
For
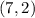
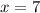 and
and
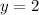
Substitute 7 for x and 2 for y in




This point is not on the graph
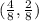
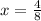 and
and
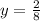
Substitute
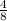 for x and
for x and
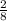 for y in
for y in

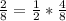
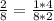


This point is on the graph