Question

4x^2 = − 9x − 4 quadratic

Answer 1

Yes, see the explanation.

Roots:

x =
`(63)/(8)`, or x= -10

Explanation:

A quadratic fomrual in standard form is;

ax^(2) + bx + c = 0

The given equation:

4x^2 = -9x - 4

Maniplate the equation using inverse operations

4x^2 = -9x - 4

-4x^2 -4x^2

0 = -4x^2 - 9x - 4

Yes, this is a quadratic equation, because it fits the requirement of being able to be written in standard form.

Now find its roots:

-4x^2 -9x - 4 = 0

remember,

x =
`\frac{(-b) +- (\sqrt{b^(2) - 4ac }) }{2a}`

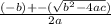
Substitute in the given values

x=
`\frac{(-(-9)) +- (\sqrt{(-9)^(2) - 4(-4)(-4)}) }{2(-4)}`

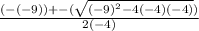
Simplify,

x =
`(9 +- (√(5184)) )/(-8)`

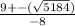
x =
`(9 +- 72)/(-8)`

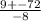
x =
`(63)/(8)`

or

x= -10