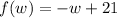Answer:
(a)
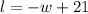
(b) Domain:
 (See attachment for graph)
(See attachment for graph)
(c)
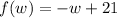
Explanation:
Given
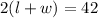
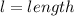
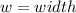
Solving (a): A function; l in terms of w
All we need to do is make l the subject in
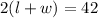
Divide through by 2
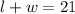
Subtract w from both sides
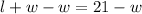
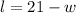
Reorder
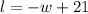
Solving (b): The graph
In (a), we have:
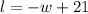
Since l and w are the dimensions of the fence, they can't be less than 1
So, the domain of the function can be
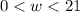
--------------------------------------------------------------------------------------------------
To check this
When
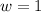

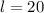
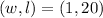
When
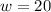
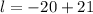

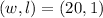
--------------------------------------------------------------------------------------------------
See attachment for graph
Solving (c): Write l as a function
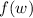
In (a), we have:
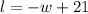
Writing l as a function, we have:
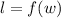
Substitute
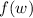 for l in
for l in
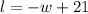
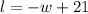 becomes
becomes