Answer:
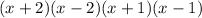
Explanation:
We want to factor the expression
 .
.
First, notice that this is in quadratic form. In other words, both the exponents have even power.
Therefore, we can make a substitution to simplify the expression.
So, let’s let
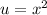 .
.
Our expression is the same as:
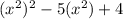
Substitute:
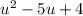
Now, we can factor like normal. We can use -1 and -4. Therefore:
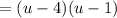
We can now substitute back u:
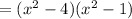
Both of these can be factored furthered using the difference of two squares:
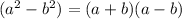
Therefore, we will have:
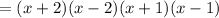
And we are done!