Question

How much will a sum of ¥4000 amount to in 1 1/2 yrs at 10% per annum compound interest,interest being paid half-yearly​

Answer 1

¥4630.50

Explanation:

Here,

• P = ¥4000
• n = 1 1/2 = 3/2 years
• r = 10% per annum

ATQ, as well,the interest is payable in half-yearly.

We know that,

• [By this formula,it could easily solved]

`\boxed{\rm \: A = P \bigg(1+ \cfrac{ \cfrac{r}{2} }{100} \bigg) {}^(2n) }`

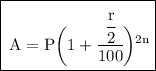
Substitute the values

`A = 4000 \bigg(1 + \cfrac{5}{100} \bigg) {}^{2 * (3)/(2) }`

Now solve.

`A = 4000 * (21/20)^3`

`\implies \: A = 4000 * \cfrac{21}{20} * \cfrac{21}{20} * \cfrac{21}{20} = \cfrac{21 * 21 * 21}{2}`

`\implies \: A = \: \yen \: 4630.50`

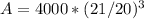
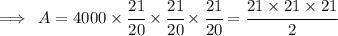
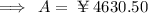
Hence,the sum of ¥ 4000 will be amounted to ¥4630.50 in 1 1/2 years.

`\rule{225pt}{2pt}`

This question arises:Why we used that formula?

Reason:

The compound interest is calculated half-yearly, the formula changes a little.In this case for r we write r/2 and for n we write 2n because a rate of r% per annum is r/2% half-yearly and n years = 2n half year So this is the reason.

Answer 2

¥4630.50

Explanation:

Compound Interest Formula

`\large \text{$ \sf A=P(1+(r)/(n))^(nt) $}`

where:

• A = final amount
• P = principal amount
• r = interest rate (in decimal form)
• n = number of times interest applied per time period
• t = number of time periods elapsed

Given:

• P = 4000
• r = 10% = 0.1
• n = 2
• t = 1.5

Substitute the given values into the formula and solve for A:

`\implies \sf A=4000\left(1+(0.1)/(2)\right)^(2 * 1.5)`

`\implies \sf A=4000\left(1.05\right)^(3)`

`\implies \sf A=4630.50`