Remember Coulomb's law: the magnitude of the electric force F between two stationary charges q₁ and q₂ over a distance r is
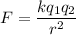
where k ≈ 8,98 × 10⁹ kg•m³/(s²•C²) is Coulomb's constant.
8.1. The diagram is simple, since only two forces are involved. The particle at Q₂ feels a force to the left due to the particle at Q₁ and a downward force due to the particle at Q₃.
8.2. First convert everything to base SI units:
0,02 µC = 0,02 × 10⁻⁶ C = 2 × 10⁻⁸ C
0,03 µC = 3 × 10⁻⁸ C
0,04 µC = 4 × 10⁻⁸ C
300 mm = 300 × 10⁻³ m = 0,3 m
600 mm = 0,6 m
Force due to Q₁ :
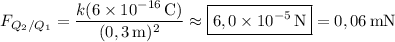
Force due to Q₃ :
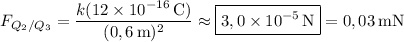
8.3. The net force on the particle at Q₂ is the vector
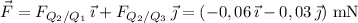
Its magnitude is
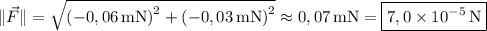
and makes an angle θ with the positive horizontal axis (pointing to the right) such that
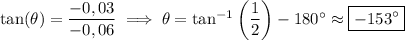
where we subtract 180° because
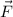 terminates in the third quadrant, but the inverse tangent function can only return angles between -90° and 90°. We use the fact that tan(x) has a period of 180° to get the angle that ends in the right quadrant.
terminates in the third quadrant, but the inverse tangent function can only return angles between -90° and 90°. We use the fact that tan(x) has a period of 180° to get the angle that ends in the right quadrant.