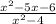Question

Help pls!
Which rational function has zeros at x = -1 and x = 6 ?

Answer 1

first option

Explanation:

the zeros are determined by the numerator of the rational function.

given that the zeros are x = - 1 and x = 6 , then the corresponding factors are

(x + 1) and (x - 6) , that is

(x + 1)(x - 6) ← expand using FOIL

= x² - 5x - 6

the rational function is then

f(x) =
`(x^2-5x-6)/(x^2-4)`

Answer 2

`f(x) = (x^(2) -5x-6)/(x^(2) -4)`

Explanation:

Let's factorize the 1st option :

⇒
`f(x) = (x^(2) -5x-6)/(x^(2) -4)`

⇒
`f(x) = (x^(2)+x-6x-6 )/((x+2)(x-2))`

⇒
`f(x) = ((x+1)(x-6))/((x+2)(x-2))`

===============================================================

Finding the zeros :

⇒ Factors of numerator should be equated to 0

1. x + 1 = 0 ⇒ x = -1
2. x - 6 = 0 ⇒ x = 6

=============================================================

Solution :

`f(x) = (x^(2) -5x-6)/(x^(2) -4)`