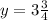Answer:
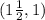 - False
- False
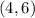 - True
- True
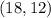 -- False
-- False
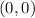 -- True
-- True
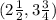 -- True
-- True
Explanation:
The points are
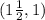 ,
,
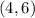 ,
,
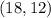 ,
,
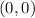 and
and
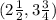 ---- missing from the question
---- missing from the question
Given
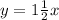
Required
Determine if each of the points would be on
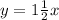
To do this, we simply substitute the value of x and of each point in
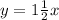 .
.
(a)
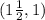
In this case;
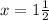 and
and
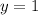
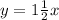 becomes
becomes
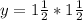
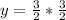
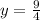
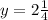
The point
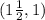 won't be on the graph because the corresponding value of y for
won't be on the graph because the corresponding value of y for
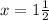 is
is
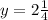
(b)
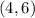
In this case;
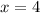

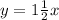 becomes
becomes
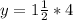
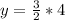
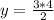
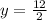

The point
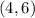 would be on the graph because the corresponding value of y for
would be on the graph because the corresponding value of y for
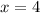 is
is

(c)
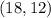
In this case:
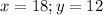
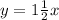 becomes
becomes
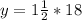
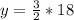

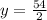
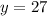
The point
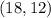 wouldn't be on the graph because the corresponding value of y for
wouldn't be on the graph because the corresponding value of y for
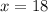 is
is

(d)
In this case;
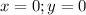
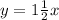 becomes
becomes
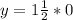
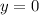
The point
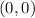 would be on the graph because the corresponding value of y for
would be on the graph because the corresponding value of y for
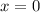 is
is
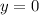
(e)
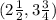
In this case:
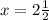 ;
;
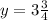
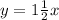 becomes
becomes
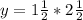
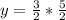
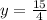
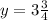
The point
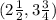 would be on the graph because the corresponding value of y for
would be on the graph because the corresponding value of y for
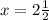 is
is