♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
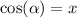
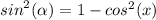
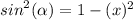
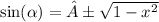
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Look :
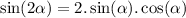
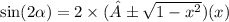
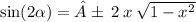
________________________________
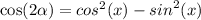
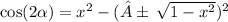
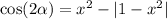
If | 1 - x² | ≥ 0 :
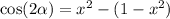
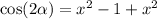
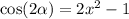
If | 1 - x² | < 0 :

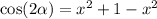
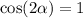
_________________________________
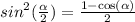
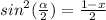
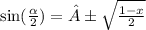
_________________________________
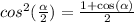
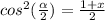
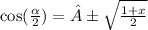
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Thus the correct answer is (( D )) .
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️