♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
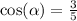
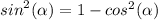
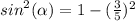
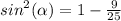
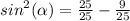
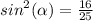
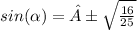
In Quadrant IV , sin is negative .
Thus ;
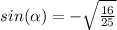
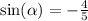
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
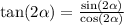
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
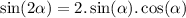
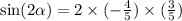
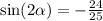
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
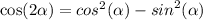
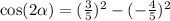
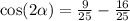
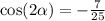
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
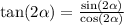
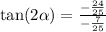
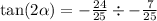
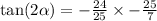
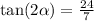
Thus the correct answer is (( C )) .
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️