Given:
The inequality is
 ...(i)
...(i)
The variables a and b are consecutive perfect squares.
To find:
The values of a and b.
Solution:
We know that, perfect square of natural numbers are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ...
Clearly, 50 lines between two consecutive perfect square 49 and 64.
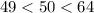
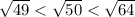 ...(ii)
...(ii)
On comparing (i) and (ii), we get
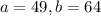
Therefore, the values of a and b are 49 and 64 respectively.