Hello!
The best way to solve this is to replace X for Y, and Y for X.
---------------------------------------------
A sample problem to help:
4x +8 = y
4y +8 = x (switched X and Y)
Y + 8 = 1/4x (solve for Y)
-8 -8
y = 1/4x -8
(now your almost done, since this is function, we need to change y to be f(x))
f(x) = 1/4 - 8
---------------------------------------------
Now that you have a basic understanding, let's do the ones you listed!
We are looking to see if the equations are inverses of the equation.
---------------------------------------------------------------------------------------------
1. f(x) = 2/3x - 7 g(x) = 3/2x + 7
First: You use equation f(x), and change f(x) to y:
y = 2/3x - 7
Next: You switch x and y:
x = 2/3y - 7
Now solve for y.
x = 2/3y - 7
+7 +7
x + 7 = 2/3y
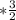
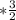
y =
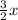 + 5
+ 5
(Set it to f(x) )
f(x) =
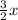 + 5
+ 5
Now look to see if it matches with the second equation.
f(x) =
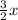 + 5 g(x) = 3/2x + 7
+ 5 g(x) = 3/2x + 7
It doesn't, so it is not the inverse of each other.
---------------------------------------------------------------------------------------------
2. f(x) = -2x - 1 f(x) =-1/2x - 1/2
First: You use equation f(x), and change f(x) to y:
y = -2x - 1
Next: You switch x and y:
x = -2y - 1
Now solve for y.
x = -2y - 1
+1 +1
x + 1 = -2y
/-2 /-2
-1/2x + 1/2 = y
(Set it to f(x) )
f(x) = -1/2x + 1/2
Now look to see if it matches with the second equation.
f(x) = -1/2x + 1/2 f(x) =-1/2x - 1/2
It does, so it is the inverse of each other.
---------------------------------------------------------------------------------------------
3. f(x) =
 g(x) = 2x - 1
g(x) = 2x - 1
First: You use equation f(x), and change f(x) to y:
y =

Next: You switch x and y:
x =
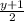
Now solve for y.
x =
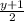
*2 *2
2x = y + 1
-1 -1
y = 2x - 1
(Set it to f(x) )
f(x) = 2x - 1
Now look to see if it matches with the second equation.
f(x) = 2x - 1 g(x) = 2x - 1
It does, so it is the inverse of each other.
---------------------------------------------------------------------------------------------
#Team Trees #Team Seas #PAW #Spread_Positivity
I hope this helps,
-Oceanbreeze24