Question

Triangle ABC is similar to XYZ. If a = 24, what are x and y?

Answer 1

x = 16

y = 105°

Explanation:

Given:

∆ABC ~ ∆XYZ

a = 24

Required:

Value of x and y

Solution:

Since ∆ABC ~ ∆XYZ, therefore:

<A ≅ <X

<B ≅ <Y

<C ≅ <Z

Also, the ratio of their Corresponding sides will be the same. That is,

`(21)/(14) = (15)/(10) = (24)/(x)`

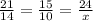
Find the value of x using,

`(15)/(10) = (24)/(x)`

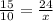
Cross multiply

`15*x = 24*10`

`15x = 240`

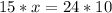
Divide both sides by 15

`x = (240)/(15)`

`x = 16`

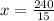
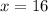
y = 180° - 75°(linear pair/angles on a straight line theorem)

y = 105°