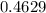Answer:
The probability is
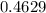
Explanation:
We know that in New South Wales, each adult on the electoral roll has a 10 % of being called up for jury duty in any year.
We can write this probability as :
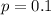
We also know that a company has 25 employees on the electoral roll.
We can write this as :

Now we can assume that this is a Bernoulli process in which the election of a random adult is independent and also the probability of being called remains the same
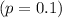
We also define the Binomial random variable in the Bernoulli process that counts the number of successes given that we set a number of individual experiments.
In this exercise, we will call a ''success'' when an adult is being called up for jury duty. We also set the number of experiments to
 (being this number the total employees of the company).
(being this number the total employees of the company).
We define the random variable as :
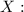 '' Number of employees being called up for jury duty in any year from the total of 25 employees ''
'' Number of employees being called up for jury duty in any year from the total of 25 employees ''
⇒
 ~ Bi ( n , p ) ⇒
~ Bi ( n , p ) ⇒
 ~ Bi ( 25 , 0.1 )
~ Bi ( 25 , 0.1 )
This means that
 can be modeled as a Binomial random variable with parameters ''n'' and ''p''.
can be modeled as a Binomial random variable with parameters ''n'' and ''p''.
We can calculate probabilities using the following equation :
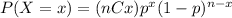
Where
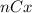 is the combinatorial number define as :
is the combinatorial number define as :

We want to calculate
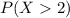 ⇒
⇒
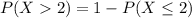 ⇒
⇒
![P(X>2)=1-[P(X=0)+P(X=1)+P(X=2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/natfs4ud9rp0pr0n7x7dgsv1jv6t7jk6hj.png)
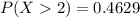
We found out that the probability is