♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
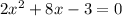
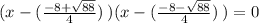
Thus ;
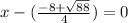

This is one of the roots.
The other root is :
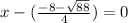

So sum of the roots is :
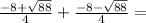
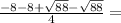
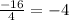
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
We have faster way to find ;
Remember from now on ,
If the quadratic functions have two roots ,
Sum of the roots is finding by following equation :
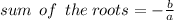
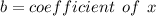

So ;
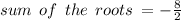
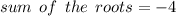
Done...
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️