Answer:
The answer is 2
Explanation:
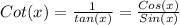
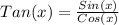
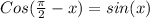
This means that

This will be a long one to solve
-> apply cos identity to right side
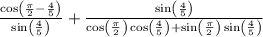
-> simplify according to unit circle
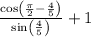
->apply cos identity again
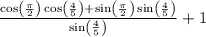
If you apply for unit circle numbers,
you will get 2
I do not recommend using a calculator for these questions, but instead, turn the form into
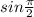 other base unit circle locations, and most likely this is the method that your teacher counts as "right."
other base unit circle locations, and most likely this is the method that your teacher counts as "right."
when using a calculator, it tends to "round" the number, which result in a inaccurate answer