Answer:
The length of the bridge is 126.492 feet.
Explanation:
Let
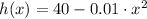 , where
, where
 is the position from the middle of the bridge, measured in feet, and
is the position from the middle of the bridge, measured in feet, and
 is the height of the bridge at a location of x feet, measured in feet. In this case, the length of the bridge is represented by the distance between the x-intercepts of the parabola, which we now find by factorization:
is the height of the bridge at a location of x feet, measured in feet. In this case, the length of the bridge is represented by the distance between the x-intercepts of the parabola, which we now find by factorization:
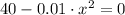 (Eq. 1)
(Eq. 1)
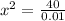
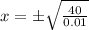
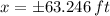
Given that the parabola is symmetrical with respect to y-axis, then the length is two times the magnitude of the value found above, that is:
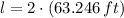
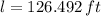
The length of the bridge is 126.492 feet.