Question

Greta is taking a road trip from Cincinnati to San Francisco. On the first day, she drove 650 miles in 10 hours. On the second day, she got a later start and drove 540 miles in 8 hours. How many miles per hour faster was her average speed the second day? Write your answer as a decimal or a whole number.

Answer 1

Given:

On the first day, she drove 650 miles in 10 hours.

On the second day, she got a later start and drove 540 miles in 8 hours.

To find:

Difference between average speed of second day and first day.

Solution:

We know that,

`Speed=(Distance)/(Time)`

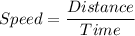
On the first day, she drove 650 miles in 10 hours. So, the average speed is

`Speed=(650)/(10)`

`Speed=65`

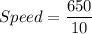
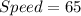
So, the average speed on first day is 65 miles per hour.

On the second day, she got a later start and drove 540 miles in 8 hours.

`Speed=(540)/(8)`

`Speed=67.5`

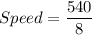
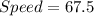
So, the average speed on second day is 67.5 miles per hour.

Difference between average speed is

`67.5-65=2.5`

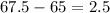
Therefore, the average speed on the second day is 2.5 miles per hour is faster than first day.