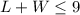Answer:
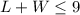
Explanation:
Given
Represent lifeguarding cars with L
Represent washing cars with W
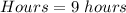 --- at most
--- at most
Required
Express the scenario as an inequality
First, we need to determine the number of hours Lauren can work.
This is calculated as follows:

From the question, we understand that the total hours cannot exceed 9 hours.
This can be expressed as
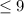
So, we have:
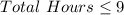
Substitute L + W for Total Hours