Question

Mean scores for elementary schools had 1228 and a standard deviation of 82. What would be the z-score for an elementary school whose mean score was 1300

Answer 1

The z-score for an elementary school with a mean score of 1300 is approximately 0.878.

Step-by-step explanation:

To calculate the z-score for an elementary school with a mean score of 1300, we need to use the formula:

z = (x - mean) / standard deviation

Plugging in the values, we get:

z = (1300 - 1228) / 82

z = 72 / 82

z = 0.878

So the z-score for the elementary school with a mean score of 1300 is approximately 0.878.

Answer 2

The z-score for an elementary school whose mean score was 1300 is 0.878

Step-by-step explanation:

The z-score can be calculated from the formula

`z = (x - \mu)/(\sigma)`

Where
`z` represents the z score

`x` represents the score

`\mu` is the mean

and
`\sigma` is the standard deviation

From the question,

Mean scores for elementary schools had 1228 and a standard deviation of 82, that is

`\mu = 1228`

`\sigma = 82`

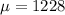
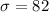
To determine the z-score (
`z`) for an elementary school whose mean score was 1300, that is

`x = 1300`

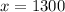
Hence, the z-score is

`z = (x - \mu)/(\sigma)`

`z = (1300 - 1228)/(82)`

`z = (72)/(82)`

`z = 0.878`

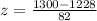
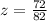
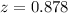
Hence, the z-score for an elementary school whose mean score was 1300 is 0.878.