Given:
The function is
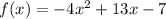
To find:
The interval on which the function is increasing.
Solution:
We have,
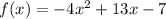
Differentiate with respect to x.
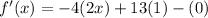

Equate f'(x)=0.
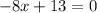
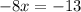
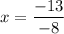

The point x=1.625 divides the number line in two parts
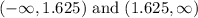 .
.
f'(x) is positive for
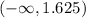 . It means the function is increasing on this interval.
. It means the function is increasing on this interval.
f'(x) is negative for
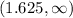 . It means the function is decreasing on this interval.
. It means the function is decreasing on this interval.
At x=1.625, f'(x) is 0. It is turning point so it will included in both intervals.
Therefore, the function is increasing on
![(-\infty, 1.625]](https://img.qammunity.org/2021/formulas/mathematics/high-school/v7vrkutgegb11vl9cj04804skjr2i6c9ua.png) .
.