Answer:
The equation of the line through the point (2, 5) that cuts off the least area from the first quadrant is
 .
.
Explanation:
From Analytical Geometry we get that the equation of the line is represented by:
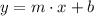 (Eq. 1)
(Eq. 1)
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
From (Eq. 1) we find that intercepts are:
x-Intercept

y-Intercept
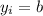
And the area done by the line in the first quadrant is:

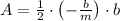
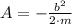 (Eq. 2)
(Eq. 2)
If we know that
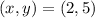 , then the equation of the line is reduced into this:
, then the equation of the line is reduced into this:
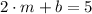
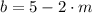 (Eq. 3)
(Eq. 3)
And we apply (Eq. 3) in (Eq. 2):
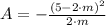
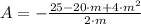
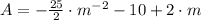 (Eq. 4)
(Eq. 4)
The first and second derivatives are, respectively:
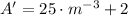 (Eq. 5)
(Eq. 5)
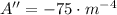 (Eq. 6)
(Eq. 6)
Then the first derivative is equalized to zero and solved:
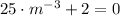
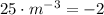
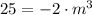
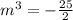
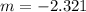
And the second derivative is evaluated at critical value:
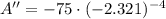
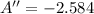
The critical value is associated with a positive area. Then, the y-intercept is: (
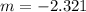 )
)
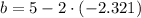
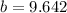
Therefore, the equation of the line through the point (2, 5) that cuts off the least area from the first quadrant is
 .
.