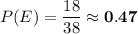Question

a roulette wheel has 38 slots numbered 1 to 36 and 0 to 00. the zeros are green. 18 of the slots are red and the rest are black. a gambler spins the wheel and drops a ball onto it. the ball is equally likely to land in each slot when the wheel stops. If a gambler bets $1 on red, they win $2 if the ball lands on red. WHat is the probability that the ball stops on red on one spin of the wheel

Answer 1

`(18)/(38) \approx \bold{0.47}`

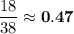
Explanation:

Given that,

Total number of slots = 38

0 and 00 are green.

Remaining number of slots = 38 - 2 = 36

18 of the 36 slots are colored red.

Rest number of slots = 36 - 18 = 18, are colored black.

The wheel spins once.

To find:

Probability that the ball stops on red.

Solution:

Formula for probability of an event E is given as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

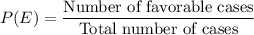
Here, number of favorable cases is equal to the number of red slots.

Number of red slots = 18

Total number of cases = 38

`P(E) = (18)/(38) \approx \bold{0.47}`