Question

A simple harmonic oscillator consists of a block of mass 45 g attached to a spring of spring constant 240 N/m, oscillating on a frictionless surface. If the block is displaced 3.5 cm from its equilibrium position and released so that its initial velocity is zero, what is its maximum velocity

Answer 1

The maximum velocity of the block is 2.56 m/s.

Step-by-step explanation:

Given;

mass of the block, m₁ = 45g = 0.045 kg

spring constant, k = 240 N/m

displacement of the block, x = 3.5 cm = 0.035 m

Apply the principle of conservation of energy;

P.E = K.E

¹/₂kx² = ¹/₂m(v-u)²

where;

v is the maximum velocity of the block

u is the initial velocity of the block, u = 0

¹/₂kx² = ¹/₂mv²

kx² = mv²

`v^2 = (kx^2)/(m)\\\\v = \sqrt{(kx^2)/(m)}\\\\v = \sqrt{((240) (0.035)^2 )/(0.045)} \\\\v = 2.56 \ m/s`

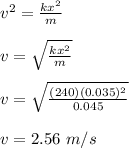
Therefore, the maximum velocity of the block is 2.56 m/s.