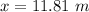Answer:
The value is
Step-by-step explanation:
From the question we are told that
The height is h = 2.0 m
The height of the window is
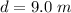
The initial velocity of the rock is
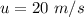
The angle at which it is thrown is
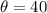
Generally the vertical component of the velocity of the stone is mathematically represented as
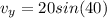
=>
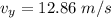
Generally the height of the window from the ground is mathematically represented as using kinematic equation as

=>
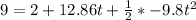
Here g is negative -9.8 m/s^2 because the direction of the stone is against gravity
So
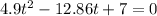
Solving this quadratic equation using quadratic formula we obtain
t = 0.770 s
Generally the velocity of the stone on the x axis is mathematically represented as
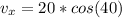
=>
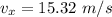
Generally the distance between the person throwing the rock and the window is mathematically represented as
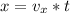
=>

=>