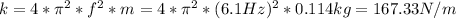Question

A positively charged objectwith a mass of 0.114 kg oscillates at the end of a spring, generating ELF (extremely low frequency) radio waves that have a wavelength of 4.92 x 107 m. The frequency of these radio waves is the same as the frequency at which the object oscillates. What is the sprinE constant of the

Answer 1

• k = 167.33 N/m

Step-by-step explanation:

• The radio waves have a fixed relationship between the propagation speed (the speed of light in vacuum), the frequency and the wavelength, as follows:
• v = c = λ*f

where c= speed of light in vacuum = 3*10⁸ m/s, λ = wavelength =

4.92*10⁷ m.

Solving for f, we get the frequency of the radio waves:

f = 6.1 Hz

• Now, from the Hooke's law, we know that the mass attached at the end of the spring oscillates with an angular frequency defined by a fixed relationship between the spring constant k and the mass m, as follows:

`\omega_(o)^(2) =(k)/(m) (1)`

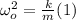
• Now, we know that there exists a fixed relationship between the angular frequency and the frequency, as follows:

`\omega = 2*\pi *f (2)`

• We also know that f in (2) is the same that we got for the radio waves, so replacing (2) in (1), and rearranging terms, we can solve for k, as follows:
• 
  `k = 4*\pi ^(2)*f^(2) *m = 4*\pi ^(2) * (6.1Hz)^(2) * 0.114 kg = 167.33 N/m`