Question

A 1500 kg car decelerates from an initial velocity of 19 m/s to a skidding stop. If the coefficient of kinetic friction is 0.100, how long are the skid marks?

Answer 1

19.4 seconds

Step-by-step explanation:

We have:

m: mass of the car = 1500 kg

v₀: is the initial speed = 19 m/s

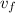`v_(f)`: is the final speed = 0 (it stops)

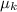`\mu_(k)`: is the coefficient of kinetic friction = 0.100

First, we need to find the acceleration by using the second Newton's law:

`\Epsilon F = ma`

`-\mu_(k)N = ma`

`-\mu_(k)mg = ma`

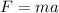
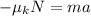
Solving for a:

`a = -\mu_(k)g = -0.1*9.81 m/s^(2) = -0.981 m/s^(2)`

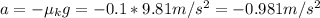
Now we can find the time until it stops:

`v_(f) = v_(0) + at`

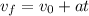
Solving for t:

`t = (v_(f) - v_(0))/(a) = (-(19 m/s))/(-0.981 m/s^(2))) = 19.4 s`

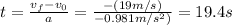
Therefore, the time until it stops is 19.4 seconds.

I hope it helps you!