Question

Liquid A has a mass density of 850.0 kg/m3 and Liquid B has a mass density of 1060.0 kg/m3. Seventy-five grams of each liquid is mixed uniformly. What is the specific gravity of the mixture

Answer 1

The specific gravity of the mixture is 0.943.

Step-by-step explanation:

The density of the mixture (
`\rho_(M)`), measured in kilograms per cubic meters, is defined by the following equation:

`\rho_(M) = (m_(A)+m_(B))/(V_(A)+V_(B))` (Eq. 1)

Where:

`m_(A)`,
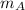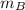`m_(B)` - Masses of liquids A and B, measured in kilograms.

`V_(A)`,
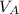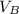`V_(B)` - Volumes of liquids A and B, measured in cubic meters.

By applying the definition of density, we expand the density of the mixture as follows:

`\rho_(M) = (m_(A)+m_(B))/((m_(A))/(\rho_(A))+(m_(B))/(\rho_(B)) )`

`\rho_(M) = (m_(A)+m_(B))/((\rho_(B)\cdot m_(A)+\rho_(A)\cdot m_(B))/(\rho_(A)\cdot \rho_(B)) )`

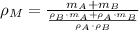
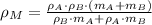`\rho_(M) = (\rho_(A)\cdot \rho_(B)\cdot (m_(A)+m_(B)))/(\rho_(B)\cdot m_(A)+\rho_(A)\cdot m_(B))` (Eq. 2)

If we know that
`\rho_(A) = 850\,(kg)/(m^(3))`,
`\rho_(B) = 1060\,(kg)/(m^(3))` and
`m_(A) = m_(B) = 0.075\,kg`, then the density of the mixture:

`\rho_(M) = (\left(850\,(kg)/(m^(3)) \right)\cdot \left(1060\,(kg)/(m^(3)) \right)\cdot (0.075\,kg+0.075\,kg))/(\left(1060\,(kg)/(m^(3)) \right)\cdot \left(0.075\,kg\right)+\left(850\,(kg)/(m^(3)) \right)\cdot \left(0.075\,kg\right))`

`\rho_(M) = 943.455\,(kg)/(m^(3))`

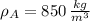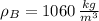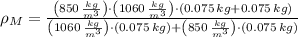
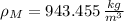
And the specific gravity is the ratio of the density of the mixture to the density of water, that is:

`SG = (\rho_(M))/(\rho_(w))` (Eq. 3)

If we get that
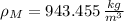`\rho_(M) = 943.455\,(kg)/(m^(3))` and
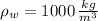`\rho_(w) = 1000\,(kg)/(m^(3))`, then the specific gravity of the mixture is:

`SG = (943.455\,(kg)/(m^(3)) )/(1000\,(kg)/(m^(3)) )`

`SG = 0.943`

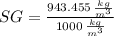
The specific gravity of the mixture is 0.943.