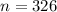Question

g Suppose the investigators had made a rough guess of 0.14 for the value of the sample standard deviation, s, before collecting data. What sample size would be necessary to obtain an interval width of 0.04 from a confidence level of 99% for a two-sided confidence interval

Answer 1

The sample size is
`n =326`

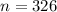
Explanation:

From the question we are told that

The rough estimate of the standard deviation is
`\sigma = 0.14`

The interval width is
`w = 0.04`

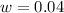
Generally the margin of error is mathematically represented as

`E = (w)/(2)`

=>
`E = (0.04)/(2)`

=>
`E = 0.02`

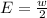
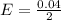
From the question we are told the confidence level is 99% , hence the level of significance is

`\alpha = (100 - 99 ) \%`

=>
`\alpha = 0.01`

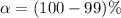
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  2.58`

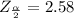
Generally the sample size is mathematically represented as

`n = [\frac{Z_{(\alpha )/(2) } *  \sigma }{E} ] ^2`

=>
`n = [( 2.58 *  0.14 )/(0.02) ] ^2`

=>
`n =326`