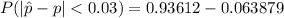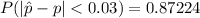Answer:
The probability is
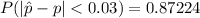
Explanation:
From the question we are told that
The population proportion is p = 0.55
The sample size is n = 639
Generally the standard deviation of this sampling distribution is mathematically represented as

=>
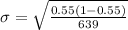
=>
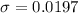
Generally the probability that the proportion of persons with a retirement account will differ from the population proportion by less than 3% is mathematically evaluated as
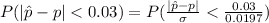


=>
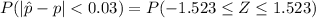
=>
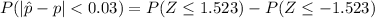
From the z table the area under the normal curve to the left corresponding to -1.523 is
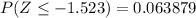
From the z table the area under the normal curve to the left corresponding to 1.523 is