Question

Jackson went into a movie theater and bought 8 bags of popcorn (x) and 2 candies (y), costing a total of $58. Cooper went into the same movie theater and bought 4 bags of popcorn (x) and 5 candies (y), costing a total of $49. Write a system of equations that could be used to determine the price of each bag of popcorn and the price of each candy. What is the price of 1 bag of popcorn and 1 candy?

Answer 1

(a)

`8x + 2y = 58`

`4x + 5y = 49`

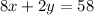
(b)

Bag of popcorn = $6

Candy = $5

Explanation:

Given

`candy = y`

`popcorn = x`

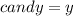
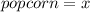
Jackson: x = 8; y= 2; Total = 58

Cooper: x = 4; y= 5; Total = 49

Solving (a): System of equation

For Jackson:

`8x + 2y = 58`

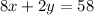
This is done by multiplying each variable by the quantity.

Same will be applied to Cooper's purchase:

Cooper:

`4x + 5y = 49`

Solving (b): Price of 1 bag of popcorn and 1 candy

This implies that we solve for x and y

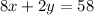`8x + 2y = 58` ----- (1)

`4x + 5y = 49` -------- (2)

Multiply the second equation by 2

`2(4x + 5y = 49)`

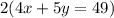
`8x + 10y = 98` -------- (3)

Subtract the (1) from (3)

`8x - 8x + 10y - 2y = 98 - 58`

`10y - 2y = 98 - 58`

`8y = 40`

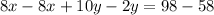
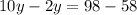
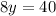
Solve for y

`y = 40/8`

`y = 5`

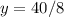
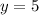
Substitute 5 for y in (1)

`8x + 2y = 58`

`8x + 2 * 5 = 58`

`8x + 10 = 58`

`8x = 58 - 10`

`8x = 48`

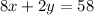
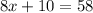
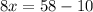
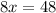
Solve for x

`x = 48/8`

`x = 6`

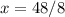
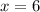
This implies:

Bag of popcorn = $6

Candy = $5