Answer:
The inductance of the inductor is 19.3 mH
Step-by-step explanation:
Inductance can be calculated from capacitive reactance,and it is given as;
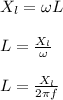
Apply ohms law to replace the capacitive reactance by voltage and current;
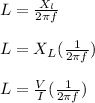
Substitute the given values;
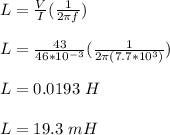
Therefore, the inductance of the inductor is 19.3 mH