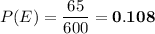Answer:
0.108
Explanation:
Given that:
Number of flights reached early = 65
Number of flights reached on time = 273
Number of flights reached late = 218
Number of flights canceled = 44
To find:
The probability that a flight is early.
Solution:
First of all, let us have a look at the formula for probability of an event E.
Formula for probability of an event E can be observed as:
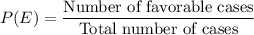
Here, Event E is that the flight is early.
Number of favorable cases is equal to the number of a flights which reached early i.e. 65
Total number of cases is the total number of flights.
i.e. 65 + 273 + 218 + 44 = 600
So, the required probability is: