Question

An apple farm yields an average of bushels of apples per tree when trees are planted on an acre of ground. Each time 1 more tree is planted per​ acre, the yield decreases by 1 bushel​ (bu) per tree as a result of crowding. How many trees should be planted on an acre in order to get the highest​ yield?

Answer 1

33 trees

Explanation:

Let us assume the number of trees planed for receiving greatest yield is be x

Now the equation would be

f(x) = (21 + x) (45 - x)

= -x^2 + 24x + 945

Now we have to differentiate the f with regard to x

`f^i (x) = -2x + 24\\\\f^i(x) = 0 = x = 12\\\\f^''(x) = -x (<0)`

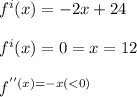
Now as it can be seen that

f is at maximum when x = 12

So, the number of trees would be

= 21 + 12

= 33 trees