Question

Solve log base 6 (x-6) - log base 6 (x + 4) = 2

Answer 1

no solutions

Explanation:

Since the two terms have the same base, we are able to use the rule for subtracting logarithms:

`log_(b)(x) - log_(b)(y) = log_(b)((x)/(y) )`

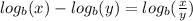
Therefore, the equation can be written as:

`log_(6)((x-6)/(x+4) )=2`

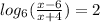
By using the definition of a logarithm we can say that:

`(x-6)/(x+4) = 6^(2)\\(x-6)/(x+4) = 36\\x -6 = 36x+144\\35x = -150\\x =-(30)/(7)`

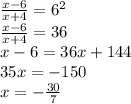
When plugging this solution in, you find that the term
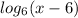`log_(6)(x-6)` has x-6 evaluate to a number less than 0. This is not included in the domain of log functions, so
`-(30)/(7)` is not a valid solution. This means that there are no solutions.