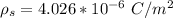Answer:
The value is
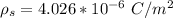
Step-by-step explanation:
From the question we are told that
The radius of the inner conductor is

The radius of the outer conductor is
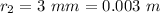
The potential at the outer conductor is
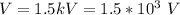
Generally the capacitance per length of the capacitor like set up of the two conductors is
![C= (2 * \pi * \epsilon_o )/( ln [(r_2)/(r_1) ])](https://img.qammunity.org/2021/formulas/physics/college/2j4yqsgkl5xgpi4atwpixk8ger4z4lun0s.png)
Here
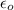 is the permitivity of free space with value
is the permitivity of free space with value
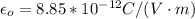
=>
![C= (2 * 3.142 * 8.85*10^(-12) )/( ln [(0.003)/(0.001) ])](https://img.qammunity.org/2021/formulas/physics/college/n8hnjd2qnhdk5dsqi1slzzty1qu6nwxio8.png)
=>

Generally given that the potential of the outer conductor with respect to the inner conductor is positive it then mean that the outer conductor is positively charge
Generally the line charge density of the outer conductor is mathematically represented as
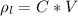
=>
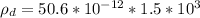
=>
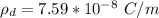
Generally the surface charge density is mathematically represented as
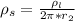 here
here

=>
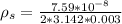
=>