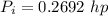Question

Water enters an ice machine at 55F and leaves as ice at 25F. If the COP of the ice machine is 3.7 during this operation, determine the required power input in horsepower for an ice production rate of 15.0 lbm/hr. Know that 169 Btu of energy needs to be removed from each lbm of water at 55F to turn it into ice at 25F.

Answer 1

The required power is
`P_i = 0.2692 \ hp`

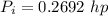
Step-by-step explanation:

From the question we are told that

The temperature of the water entering ice machine is
`T_1 = 55 ^o F`

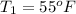
The temperature of the water leaving is
`T_2 = 25 ^oF`

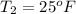
The COP of the ice machine is
`COP= 3.7`

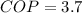
The production rate of an ice
`\r m = 15.0 \ lbm /hr`

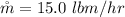
The energy that needs to removed from each lbm of water at 55 F is
`E = 169 Btu`

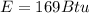
Generally the cooling load of the ice machine is mathematically represented as

`\r Q_L = \r m * E`

`\r Q_L =15 * 169`

=>
`\r Q_L = 2535 \ Btu/h`

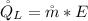
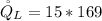
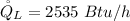
Generally the COP of the ice machine is mathematically represented as

`COP = (\r Q_L)/(P_i)`

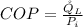
Here
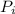`P_i` is the net power input needed to successfully run the ice machine

So

`3.7 = (2535)/(P_i)`

=>
`P_i = 685 \ Btu/h`

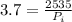
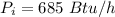
Converting to horsepower

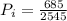
`P_i = (685)/(2545)`

=>
`P_i = 0.2692 \ hp`