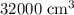Question

If 4,800 cm2 of material is available to make a box with a square base and an open top, find the largest possible volume of the box. Step 1

Answer 1

`32000\ \text{cm}^3`

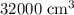
Explanation:

b = Length and breadth of base

h = Height of box

Surface area of box =
`4800\ \text{cm}^2`

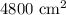
Volume is given by

`V=b^2h`

Surface area is given by area of base plus the area of the four sides

`b^2+4hb=4800\\\Rightarrow h=(4800-b^2)/(4b)\\\Rightarrow h=(1200)/(b)-(b)/(4)`

`V=b^2h=b^2((1200)/(b)-(b)/(4))\\\Rightarrow V=1200b-(b^3)/(4)`

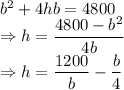
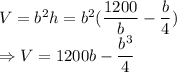
Differentiating with respect to the base dimensions we get

`(dV)/(db)=1200-(3)/(4)b^2`

Equating with 0

`0=1200-(3)/(4)b^2\\\Rightarrow b=\sqrt{(1200* 4)/(3)}\\\Rightarrow b=40\ \text{cm}`

Finding the double derative

`(d^2V)/(db^2)=-(3)/(2)b`

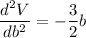
at
`b=40`

`(d^2V)/(db^2)=-(3)/(2)b=-(3)/(2)* 40=-60\\ -60<0`

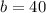
So, the maximum value of b is 40 cm

`h=(1200)/(b)-(b)/(4)=(1200)/(40)-(40)/(4)\\\Rightarrow h=20\ \text{cm}`

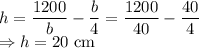
Volume is given by

`V=b^2h=40^2*20\\\Rightarrow V=32000\ \text{cm}^3`

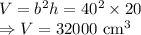
The largest possible volume of the box is
`32000\ \text{cm}^3`