Question

A researcher is evaluating the influence of a treatment using a sample selected from a normally distributed population with a mean of

Answer 1

The power of the test is 0.67.

Explanation:

The complete question is:

A researcher is evaluating the influence of a treatment using a sample selected from a normally distributed population with a mean of μ = 80 and a standard deviation σ = 20. The researcher expects a 12-point treatment effect and plans to use a two-tailed hypothesis test with α = 0.05. Compute the power of the test if the researcher uses a sample of n = 16 individuals .

Solution:

The information provided are:

`\mu=80\\\sigma = 20\\n = 16\\\alpha=0.05`

The expected mean is:

`\mu_(\bar x)=80+12=92`

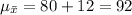
The critical z-score at α = 0.05 for a two-tailed test is:

z = 1.96

*Use a z-table.

Compute the test statistic value as follows:

`z_(\bar x)=(\mu_(\bar x)-\mu)/(\sigma_(\bar x))=(92-80)/(20/√(16))=2.4`

The power of statistical test is well-defined as the probability that we reject a false null hypothesis.

Power = Area to the right of the critical z under the assumption that H₀ is false.

Location of critical z (in H₀ is false distribution) =
`z_(\bar x)-z`

`= 2.4 - 1.96 \\= -0.44`

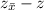
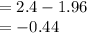
This is negative because the critical z score is to the left of the mean of the H₀ in false distribution.

Area above z = -0 .44.

Compute the value of P (Z > -0.44) as follows:

`P(Z>-0.44)=1-P(Z<-0.44)=P(Z<0.44)=0.67`

Thus, the power of the test is 0.67.