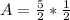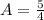Question

Hong the trainer has two solo workout plans that he offers his clients: Plan A and Plan B. Each client does either one or the other (not both). On Friday there were 4 clients who did Plan A and 8 who did Plan B. On Saturday there were 2 clients who did Plan A and 3 who did Plan B. Hong trained his Friday clients for a total of 9 hours and his Saturday clients for a total of 4 hours. How long does each of the workout plans last?

Answer 1

Session A = 1.25 hours

Session B = 0.5 hours

Explanation:

Given

Plans: A and B

Friday can be expressed as: 4A + 8B

Saturday can be expressed as: 2A + 3B

Total Time:

Friday = 9 hours

Saturday = 4 hours

Required

Determine time for each session (A and B)

The question illustrates simultaneous equation and the equations are;

`4A + 8B = 9`

`2A + 3B = 4`

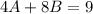
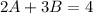
Multiply the second equation by 2

`2(2A + 3B = 4)`

`4A + 6B = 8`

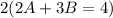
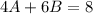
Subtract this from the first equation:

`(4A + 8B = 9) - (4A + 6B = 8)`

`4A - 4A + 8B -6B = 9 - 8`

`8B -6B = 1`

`2B = 1`

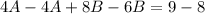
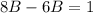
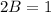
Solve for B

`B= (1)/(2)`

`B = 0.5\ hours`

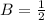
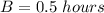
Substitute
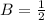`B= (1)/(2)` in
`2A + 3B = 4`

`2A + 3((1)/(2)) = 4`

`2A + (3)/(2) = 4`

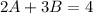
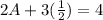
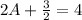
Solve for 2A

`2A = 4 - (3)/(2)`

`2A = (8 - 3)/(2)`

`2A = (5)/(2)`

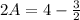
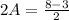
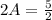
Solve for A

`A = (5)/(2) * (1)/(2)`

`A = (5)/(4)`

`A = 1.25\ hours`