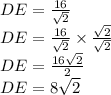Question

DEF, DF = 16 and m angle F = 45

Answer 1

`8√(2)`

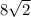
Explanation:

We can sum the angles in a triangle to 180°:

m<D + m<E + m<F = 180°

m<D + 90° + 45° = 180°

m<D = 45°

Therefore, the triangle is an isosceles right triangle, since the base angles, <F and <D are the same measure. Because the triangle is isosceles, the legs are congruent, meaning that

DE = EF

We can use the Pythagorean Theorem(
`a^(2) + b^(2) = c^(2)`) and plug in 16 as c, and DE and EF as a and b:

`DE^(2) + EF^(2) = 16^(2)`

Since DE is the same as EF, we can substitute it in:

`DE^(2) + DE^(2) = 256\\2DE^(2) = 256\\DE^(2) = 128\\DE = √(128)`

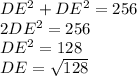
The square root of 128 is the same as
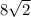`8√(2)` since 128 can be factored into 64 x 2. So
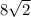`8√(2)` is the answer.

If you are looking for an easier way to do this, once you are able to recognize DEF is an isosceles triangle, you can say
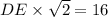`DE * √(2) = 16` as this applies to all isosceles right triangles. This simplifies to:

`DE = (16)/(√(2)) \\DE = (16)/(√(2) ) * (√(2))/(√(2) ) \\DE = (16√(2) )/(2) \\DE = 8√(2)`

Answer 2

Answer:
`8√(2)`

================================================

Work Shown:

x = length of each leg

Use the pythagorean theorem to get...

`a^2+b^2 = c^2\\\\x^2+x^2 = 16^2\\\\2x^2 = 256\\\\x^2 = 256/2\\\\x^2 = 128\\\\x = √(128)\\\\x = √(64*2)\\\\x = √(64)*√(2)\\\\x = 8√(2)\\\\`

Or as an alternative path, you can divide the hypotenuse by
`√(2)` and then rationalize the denominator.

Both of these methods apply to 45-45-90 triangles only.