Question

Subtract

−7a2+3a−9−7a 2 +3a−9minus, 7, a, squared, plus, 3, a, minus, 9 from 5a2−6a−45a 2−6a−45, a, squared, minus, 6, a, minus, 4.

Answer 1

After subtracting
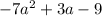`-7a^2+3a-9` from
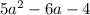`5a^2-6a-4`, the answer is:

`12a^2-9a+5`

Explanation:

The given expressions are:

Expression 1:
`-7a^2+3a-9`

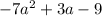
Expression 2:
`5a^2-6a-4`

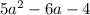
According to the question, expression 1 has to be subtracted from expression 2.

Writing it mathematically,

`expression\ 2 - expression\ 1 = (5a^2-6a-4)-(-7a^2+3a-9)`

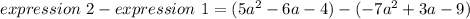
The minus between both expression, when solved, will change the signs of the terms in expression 1

So,

`= 5a^2-6a-4+7a^2-3a+9`

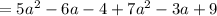
Combining alike terms(i.e. combining squared terms together and similarly linear and constant terms)

`=5a^2+7a^2-6a-3a-4+9\\=12a^2 -9a +5`

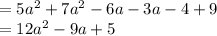
After subtracting
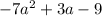`-7a^2+3a-9` from
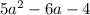`5a^2-6a-4`, the answer is:

`12a^2-9a+5`