Question

The half-life of radium-226 is about 1,590 years. How much of a 100mg sample will be left in 500 years? Write your answer rounded to the nearest tenth.

Answer 1

There will be left 80.4 of the sample in 500 years

Explanation:

Radioactive Decay Model

Suppose N is the size of a population of radioactive atoms at a given time t, No is the size of an initial population of radioactive atoms at time t = 0, and k is the decay constant, then the equation is as follows:

`N=N_o\cdot e^(-kt)`

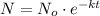
The time required for half of the original population of radioactive atoms to decay is called the half-life Th. The relationship between the half-life and the decay constant is:

`\displaystyle T_h=(ln 2)/(k)\approx(0.693)/(k)`

We know the half-life of radium-226 is about 1,590 years. We can find the value of k by solving the above equation:

`\displaystyle k=(ln 2)/(T_h)`

`\displaystyle k=(ln 2)/(1,590)`

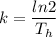
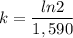
k=0.000436

The initial mass of the sample is 100 gr, thus the model for the mass at time t is:

`M(t)=100\cdot e^(-0.000436t)`

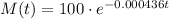
When t=500 years:

`M(500)=100\cdot e^(-0.000436*500)`

`M(500)=100\cdot 0.804`

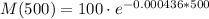
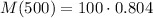
M(500)=80.4 gr

There will be left 80.4 of the sample in 500 years