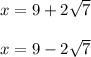Question

3. Solve for the zeros. Use the Completing the Square method.
a) f(x) = x2 – 18x + 53

Answer 1

`x=9+ 2√(7)\\x=9- 2√(7)`

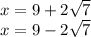
Explanation:

To solve a quadratic equation by completing squares we need to recall these basic algebra relations called the square of a binomial:

`(a+b)^2=a^2+2ab+b^2`

`(a-b)^2=a^2-2ab+b^2`

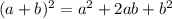
We can use them from right to left to factor trinomials:

`a^2-2ab+b^2=(a-b)^2`

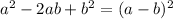
We need to solve the equation:

`x^2-18x+53=0`

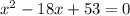
Subtracting 53:

`x^2-18x=-53`

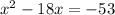
The first two terms of the left side of the equation are the first two terms of the trinomial given in the formula, having:

`a^2=x^2`

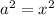
Or, equivalently:

`a=x`

Also:

`2ab=-18x`

Since a=x

`2xb=-18x`

Simplifying:

b=-9

We need to complete the square by adding
`b^2=81`

Adding 81:

`x^2-18x+81=-53+81`

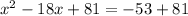
Factoring and operating:

`(x-9)^2=28`

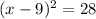
Since 28=4*7

`(x-9)^2=4*7`

Taking square roots:

`x-9=\pm √(4*7)`

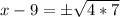
Separating the square root of 4:

`x-9=\pm 2√(7)`

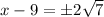
Solving:

`x=9\pm 2√(7)`

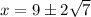
The two solutions are:

`x=9+ 2√(7)\\\\x=9- 2√(7)`