Question

The radius of the base of a cylinder is decreasing at a rate of 9 millimeters per hour and the height of the cylinder is increasing at a rate of 2 millimeters per hour. At a certain instant, the base radius is 8 millimeters and the height is 3 millimeters. What is the rate of change of the surface area of the cylinder at that instant in square millimeters per hour?

a) 310pi
b) 155pi
c) -155pi
d) -310pi

Answer 1

Answer: d) -310pi

Explanation:

Instantaneous Rate of Change

Is the change in the rate of change of a function at a particular instant. It's the same as the derivative value at a specific point.

The surface area of a cylinder of radius r and height h is:

`A=2\pi r^2+2\pi r h`

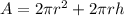
We need to calculate the rate of change of the surface area of the cylinder at a specific moment where:

The radius is r=8 mm

The height is h=3 mm

The radius changes at r'=-9 mm/hr

The height changes at h'=+2 mm/hr

Find the derivative of A with respect to time:

`A'=2\pi (r^2)'+2\pi (r h)'`

`A'=2\pi 2rr'+2\pi (r' h+rh')`

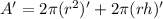
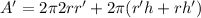
Substituting the values:

`A'=2\pi 2(8)(-9)+2\pi ((-9) (3)+(8)(2))`

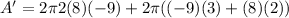
Calculating:

`A'=-288\pi +2\pi (-27+16)`

`A'=-288\pi +2\pi (-11)`

`A'=-288\pi -22\pi`

`A'=-310\pi`

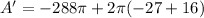
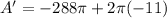
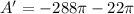
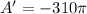
Answer: d) -310pi