Question

Tim and his sister chloe are both saving money to buy cell new phones. The Graph shows the amount of money in each acc based on the number of weeks

Answer 1

a. The equation for the line representing Tim's account is y = 10·x + 40

b. The equation for the line representing Chloe's account is y = 20·x + 10

c. The solution to the system of equations is x = 3, y = 70

Explanation:

a. The y-intercept of the graph for Tim's account = (0, 40)

A second point on the line graph of Tim's account = (3, 70)

The slope, m of a straight line equation, given two points on the line, (x₁, y₁), (x₂, y₂) is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

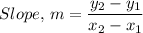
Therefore, the slope, m = (70 - 40)/(3 - 0) = 10

The equation for the line representing Tim's account in slope and intercept form is y = 10·x + 40

b. The y-intercept of the graph for Chloe's account = (0, 10)

A second point on the line graph of Chloe's account is also = (3, 70)

Therefore, the slope of the equation representing Chloe's account, m is given as follows;

m = (70 - 10)/(3 - 0) = 20

The equation for the line representing Chloe's account in slope and intercept form is y = 20·x + 10

c. The solution is found at the point where the two lines meet (are equal) as follows;

For Tim's account y = 10·x + 40

For Chloe's account y = 20·x + 10

Equating both equations gives;

y = y and 10·x + 40 = 20·x + 10

From which we have;

40 - 10 = 20·x - 10·x = 10·x

30 = 10·x

x = 30/10 = 3

x = 3

Therefore, haven found the x-coordinate value, the y-coordinate of the point which is the solution (where the two equations are equal or the two line graphs cross) of the two equations is given as follows;

y = 10·x + 40 where, x = 3, we have;

y = 10 × 3 + 40 = 70

y = 70

The point of the solution of the system of equations is (3, 70)

The solution to the system of equations is x = 3, y = 70.