Question

Find the sum and the product of the roots of the equation: x^2+35x−51=0

Answer 1

The first step will be to find the roots of the equation:

x^2 + 35*x - 51 = 0.

We know that for a quadratic equation like:

a*x^2 + b*x + c = 0

The solutions are:

`x = (-b +- √(b^2 - 4*a*c) )/(2*a)`

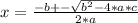
In this case we have:

a = 1

b = 35

c = -51

Then the solutions are:

`x = (-35 +- √((-35)^2 - 4*1*(-51)) )/(2*1) = (-35 +- √(1429) )/(2)`

Then the two solutions are:

x1 = (-35 + √(1429))/2

x2 = (-35 - √(1429))/2

The sum will be:

S = x1 + x2 = (-35 + √(1429))/2 + (-35 - √(1429))/2

= (-35 + √(1429) - 35 - √(1429))/2 = -35

The product will be:

P = x1*x2 = ( (-35 + √(1429))/2)*( (-35 - √(1429))/2)

= (-35 + √(1429))*(-35 - √(1429))/4

= (35*√(1429) + 35^2 + 1429 - 35*√(1429))/4

= (1225 + 1429)/4 = 663.5