Question

Hi, I need help again T^T

Answer 1

It’s think it’s A I’m not sure

Answer 2

A) 60 feet.

Explanation:

We know that it’s a rectangular swimming pool with a length of 48 feet and a width of 36 feet.

In order for the hose to be extended from the southwest corner to the northewest corner for the shortest length, the hose must be perfectly straight.

Therefore, the the hose will form a hypotenuse.

In other words, the shortest length will simply be the length of the diagonal of the rectangle.

We can find the length of the diagonal using the Pythagorean Theorem, namely:

`a^2+b^2=c^2`

Where a and b are the side lengths, and c is the length of the hypotenuse or in this case the diagonal.

So, substitute 48 for a and 36 for b:

`(48)^2+(36)^2=c^2`

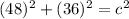
Evaluate:

`2304+1296=c^2`

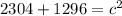
Add:

`c^2=3600`

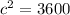
Take the square root of both sides:

`c=60\text{ feet}\\`

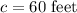
Therefore, the shortest length for the hose is 60 feet.