Question

SOMEONE HELP ME PLS I NEED HELP

Answer 1

`m\angle{W} = {75{^\circ}}`

`m\angle{Y} = {15{^\circ}}`

`m\angle{Z} = {90{^\circ}}`

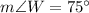
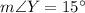
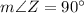
Explanation:

All angles in a triangle must add up to
`180{^\circ}`

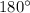
First we can use an equation to find
`x`

`(x - 15) + (2x - 165) + 90 = 180`

`3x - 180 = 90`

`3x = 270`

`x = 90`

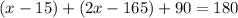
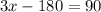
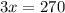
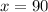
Now we can solve for
`\angle W`and
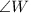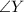`\angle Y` through substitution

`\angle{W} = 90 - 15 \rightarrow \boxed{75{^\circ}}`

`\angle{Y} = 2x - 165 \rightarrow 2(90) - 165 \rightarrow 180 - 165 \rightarrow \boxed{15{^\circ}}`

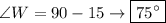
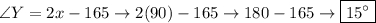
Now we can classify the triangle

It is right because it has a
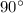`90{^\circ}` angle

These are the answers

- Kan Academy Advanced